Resumos LEIC-A
IST LEIC-AGitHub
Edit page

Árvores de Decisão

O que são Árvores de Decisão?

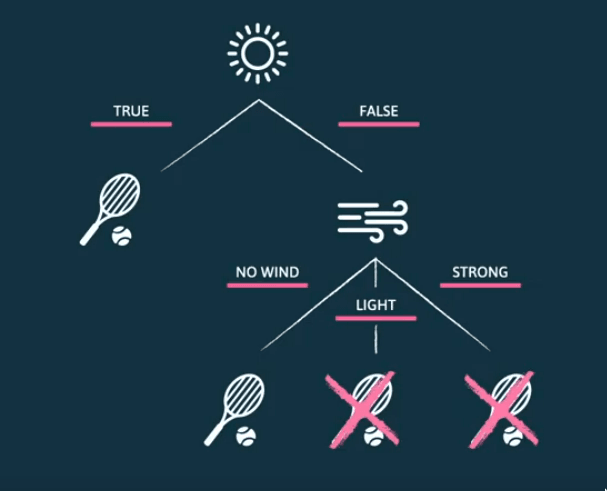
As árvores de decisão (decision trees) são um modelo de decisão original do machine learning simbólico. Estas são representadas por um grafo sem ciclos, onde um nó representa um teste a um valor assumido por uma variável. Assim, cada nó corresponde a uma proposição lógica. Cada nó tem tantas arestas, ou ramos, quantos os valores a variável pode assumir. Os nós terminais são folhas e representam os valores assumidos pela variável de destino, a classe. Cada ramo pode ser visto como uma conjunção de proposições, daí a sua origem no machine learning simbolista.

Árvore de Decisão

Variáveis Contínuas

O modelo foi também adaptado para lidar com variáveis numéricas. Cada nó testa desigualdades em vez de testar o valor assumido pela variável. Existe o ramo em que a desigualdade se verifica e outro em que esta não se verifica. Assim, cada nó cria uma partição do espaço de possíveis valores.

Algoritmos de Treino

Dada a natureza recursiva das árvores em que um nó pode ser uma folha ou uma raiz de uma outra árvore, os algoritmos que operam sobre este tipo de estruturas são também eles recursivos.

Na construção da árvore de decisão, se todos os registos pertencerem à mesma classe, é criada uma folha, rotulada com essa classe. Caso contrário, cria-se um nó com a melhor variável para discriminar entre as classes (a variável mais relevante). De seguida, divide-se o conjunto de dados consoante a escolha realizada, criam-se os ramos que representam cada um dos valores possíveis e repete-se o processo para cada um dos ramos.

Escolher a Melhor Variável

A escolha da próxima variável a considerar, no processo de construção de uma árvore de decisão, é de extrema importância pois condiciona o tamanho final da árvore. Existem várias métricas de escolha. Contudo todas apresentam as seguintes propriedades:

  • Devolver 00 se o nó for puro (todos os registos pertencem à mesma classe).
  • Devolver 11 se a impureza do nó for máxima (o número de registos por classe é igual).
  • Devolver x∈]0,1[x \in ]0, 1[ em caso contrário.

A métrica mais utilizada é a entropia de Shannon, baseada na teoria da informação.

Surpresa e Informação

Uma definição intuitiva de surpresa assenta no facto de, quanto menor a probabilidade de um evento ocorrer, maior é a nossa surpresa face à ocorrência desse evento. Definimos surpresa de um evento kk como o inverso da probabilidade da ocorrência deste. Por exemplo, o evento "Homem morde cão." evoca mais surpresa do que "Cão morde homem.".

sk=1p(xk)s_k = \frac{1}{p(x_k)}

A informação fornecida pela ocorrência deste evento é proporcional à surpresa. Definimos a informação dada pela ocorrência de um evento como:

Ii=log⁡2(sk)=−log⁡2(p(xk))I_i = \log_2({s_k}) = -\log_2({p(x_k)})

Como seria de esperar, na ocorrência de um evento pouco provável, temos uma maior informação, face a um evento mais provável.

Devemos notar que probabilidades são multiplicadas e a informação é somada, devido ao logaritmo. O logaritmo base 2, faz com que a informação seja representada em bits.

Entropia de Shannon

A entropia de Shannon corresponde ao número mínimo de bits necessários para representar informação.

Para x∈Xx \in X eventos diferentes, a entropia de Shannon é calculada de acordo com a fórmula seguinte.

I(x)=∑x∈Xp(x)×Ix=−∑x∈Xp(x)×log⁡2(p(x))I(x) = \sum_{x \in X} p(x) \times I_x = - \sum_{x \in X} p(x) \times \log_2{(p(x))}

Ganho de Informação (Information Gain)

O ganho de informação permite-nos escolher qual a próxima variável a considerar na construção de uma árvore de decisão.

Se, para determinada variável FxF_x, existirem kk valores possíveis, a árvore é dividida em kk subconjuntos: {X1,X2,...,Xk}\{X_1, X_2, ..., X_k\}.

Após realizarmos a partição da tabela em cada valor possível para o atributo, calculamos a entropia de cada uma destas partições. De seguida calculamos a entropia total, definida como a média ponderada das entropias de cada partição.

E(Fx)=∑i=1k#Xi#X×I(Xi)E(F_x) = \sum_{i=1}^{k} \frac{\#X_i}{\#X} \times I(X_i)

Define-se o ganho de informação como

gain(Fk)=I(X)−E(Fk)\text{gain}(F_k) = I(X) - E(F_k)

A heurística, apesar de não garantir a escolha da árvore mais simples, leva à construção de uma árvore bastante simples. Ao computar o ganho de cada variável, escolhemos aquela que apresenta um maior ganho de informação ou, de forma equivalente, a menor entropia ponderada.

Pruning

O processo recursivo de construção de uma árvore de decisão continua até à geração de um nó puro, o que tende a tornar as árvores bastante grandes. A elevada profundidade ou ramificação da árvore pode ser causada pela presença de ruído nos dados. Muitas vezes, estas ocorrências levam ao fenómeno de overfitting.

O processo de poda, ou pruning, é uma abordagem para evitar o overfitting. Esta torna as árvores menores, com o objetivo de maximizar o seu desempenho sobre dados ainda não observados. As árvores podem ser podadas a priori ou a posteriori.

Pre-Pruning

Este tipo de poda interrompe o crescimento da árvore sempre que um nó não melhore a exatidão do modelo de forma significativa, de acordo com um limite especificado.

É mais eficiente do que podar a árvore posteriormente, pois para o processo de treino mais cedo.

Post-Pruning

Neste tipo de poda, treina-se uma árvore tão grande quanto possível e depois removem-se os ramos que não fornecerem uma melhoria de exatidão estatisticamente significativa.

Overfitting

Para além do processo de poda da árvore, a limitação da profundidade da árvore permite que o modelo não se ajuste tanto aos dados de treino, permitindo uma melhor performance no conjunto de teste e evitando o overfitting.