Lazy Learning
Os analogistas defendem uma aprendizagem por analogia, também conhecida por lazy learning, onde as decisões são tomadas tendo em conta a comparação do objeto a classificar com objetos já conhecidos. Os algoritmos limitam-se a memorizar o conjunto das observações, daí o termo lazy learning.
Classificador K-Nearest Neighbors
Este classificador, também conhecido por KNN, perante um novo objeto, começa por procurar os registos mais semelhantes a este novo objeto, entre os objetos já conhecidos. Analisando os rótulos desses objetos, o novo objeto seria classificado com o rótulo apresentado pela maioria dos objetos analisados.
Para tal, os registos são classificados como pontos num plano euclidiano e o algoritmo simplesmente memoriza os dados de treino, sem qualquer pré-processamento adicional. Para encontrar os vizinhos mais próximos, computa-se uma função de distância entre cada um dos objetos e o novo objeto a classificar, com o objetivo de descobrir os pontos mais próximos.
Por não haver uma fase de treino, sendo que o algoritmo apenas memoriza os dados de treino, diz-se que o algoritmo não produz um modelo.
Número de Vizinhos
Os resultados do algoritmo dependem fortemente do número de vizinhos escolhido. Normalmente, escolhe-se experimentalmente. Começando com , avaliam-se os resultados num conjunto de validação e repete-se o processo para maiores valores de . Finalmente escolhe-se o número de vizinhos que apresenta o melhor desempenho.
Na presença de classificações binárias (com duas classes), é habitual escolher um valor ímpar de , de modo a evitar empates, no processo de classificação. Para classificações não binárias, se encontrarmos um empate, reduzimos o valor de até quebrar o empate.
Comparação
Funções de Distância
Uma função de distância permite calcular a distância entre dois pontos em . Existem várias funções de distância possíveis. Contudo, todas apresentam as seguintes propriedades.
As funções de distância mais utilizadas são casos particulares da chamada distância de Minkowski.
A distância euclidiana corresponde ao caso particular quando .
A distância de Manhattan corresponde ao caso particular quando .
A distância de Hamming é uma função utilizada para dados categóricos. Corresponde ao número de diferentes atributos em dois vetores.
Semelhança de Cossenos
Uma função de distância nem sempre é a métrica mais adequada para comparar duas observações. Imagine-se que as nossas observações descrevem documentos, cada um destes caracterizado pela frequência absoluta de certas palavras. Com o objetivo de encontrar documentos sobre temas semelhantes, uma função de distância separa dois documentos que, apesar de partilharem o mesmo tema, têm diferentes tamanhos.
A métrica da semelhança de cossenos resolveria o problema. Apesar de os dois documentos terem tamanhos diferentes, a frequência relativa de uma certa palavra chave é bastante semelhantes nos dois.
Correlação
Além das métrica de distância e da semelhança de cossenos, a proximidade de duas observações pode ainda ser expressa por diferentes coeficientes de correlação. Tais incluem o coeficiente de correlação de Pearson e o rank de Spearman.
Vizinhos à Mesma Distância
Numa situação onde vários vizinhos se encontrem à mesma distância, como podemos escolher os vizinhos? Se forem todos da mesma classe, o objeto é classificado como pertencente a essa classe. Caso contrário, o classificador não consegue escolher os vizinhos a considerar e não classifica o objeto. Perante muitos destes casos, é habitual escolher uma função de semelhança que melhor discrimine entre os objetos.
Escalas Diferentes
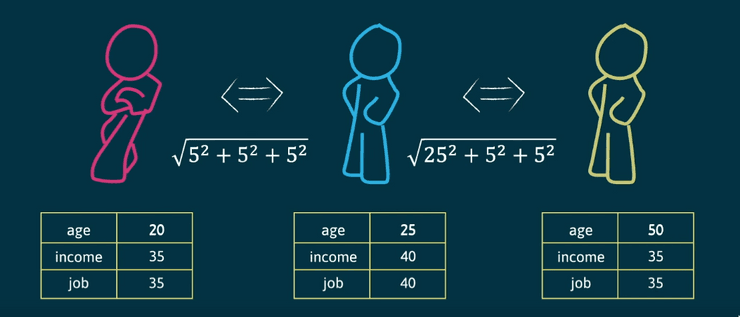
Outro problema é o de diferentes variáveis utilizarem diferentes escalas. Na figura abaixo, apesar da diferença de idades entre a pessoa vermelha e a pessoa amarela ser bastante alta, o algoritmo indica que estes objetos são mais próximos entre si, do que qualquer um destes com o objeto azul. Isto deve-se ao facto de a diferença salarial apresentar valores várias ordens de grandeza acima da diferença de idades. Para tal, normalizam-se os dados de modo a tornar estas diferenças mais próximas. O salário poderia ser representado então pelo número de milhares de unidades monetárias por ano.
Variáveis Redundantes
Um outro problema é a presença de variáveis que estejam correlacionadas com outras. No exemplo abaixo, as variáveis income e job, depois de normalizadas, apresentam a mesma informação. A presença de variáveis redundantes atribui mais peso a essas mesmas variáveis do que às outras, dificultando a discriminação entre os objetos.
KNN Ponderado
Também é possível atribuir um peso a cada um dos vizinhos consoante a sua semelhança com o objeto a classificar.
Overfitting
De modo a evitar o overfitting, o valor de vizinhos mais próximos pode ser aumentado e podem ser usados pesos uniformes, ao invés de pesos ponderados.