Algoritmos Eficientes de Ordenação

Entramos agora numa secção com alguns algoritmos de ordenação mais avançados, algoritmos estes que estarão, de uma maneira ou de outra, presentes na nossa carreira profissional.

Quick Sort

A par do merge sort, o mais "comum" de entre os algoritmos desta secção. Bastante popular devido ao quão fácil é implementá-lo, a par de um caso médio de complexidade relativamente bom. A stdlib em C oferece uma implementação nativa, qsort(), mas atenção: a docência de IAED costuma proibir o seu uso em contexto de projetos, pelo que se a quiserem usar devem consultar o enunciado dos mesmos e/ou contactar a docência.

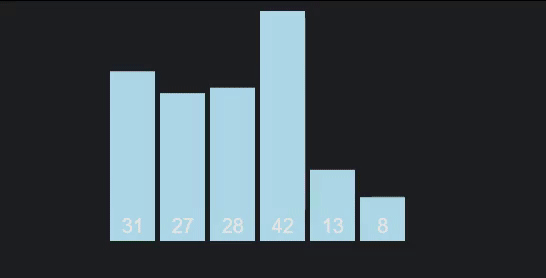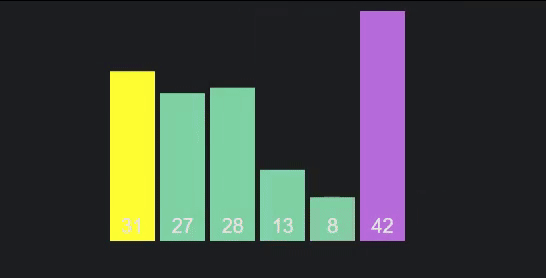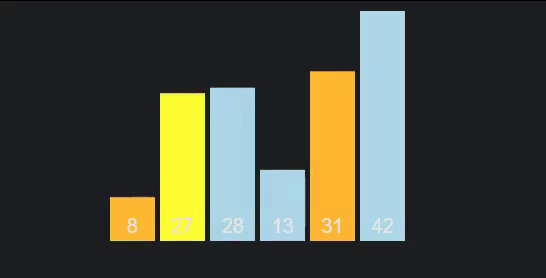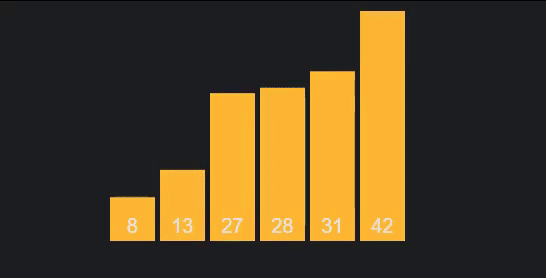
É o primeiro algoritmo que vamos estudar que segue a metodologia "dividir para conquistar", divide and conquer: a ideia chave passa por realizar partições sucessivas dos dados, e ordenar cada partição independente e recursivamente (das mais pequenas para as maiores). As partições em si são feitas ao escolher um pivô, um elemento à nossa escolha do vetor, e dividindo o vetor em duas partes: a parte da esquerda, com elementos com chave menor que a do pivô, e a da direita com elementos que possuem chave maior que ele. Estas partições são, claro, criadas recursivamente. Quando chegamos ao fim da recursão, fazemos backtracking, ordenando as partições. Por norma, o algoritmo de ordenação auxiliar utilizado para ordenar as partições é o insertion sort.

void quick_sort(Item a[], int left, int right) {
    int i;
    if (right <= left) {
        return;
    }
    i = partition(a, left, right);
    quick_sort(a, left, i - 1);
    quick_sort(a, i + 1, right);
}

int partition(Item a[], int left, int right) {
    int i = left - 1, j = right;
    Item v = a[right];
    while (i < j) {
        while (less(a[++i], v))
            ;
        while (less(v, a[--j])) {
            if (j == left) {
                break;
            }
        }
        if (i < j) {
            exch(a[i], a[j]);
        }
    }
    exch(a[i], a[right]);
    return i;
}

Pode ser difícil entender o funcionamento do algoritmo só por palavras, pelo que o vídeo abaixo pode ajuda a clarificar algumas dúvidas:

O algoritmo realiza $2n\log{n}$ trocas, possuindo complexidade temporal no pior caso quadrática. A complexidade espacial do algoritmo é também quadrática, pelo que para vetores muito grandes pode não ser ideal utilizar o quick sort. Não é um algoritmo estável.

Merge Sort

O outro algoritmo desta secção baseado na metodologia divide and conquer.

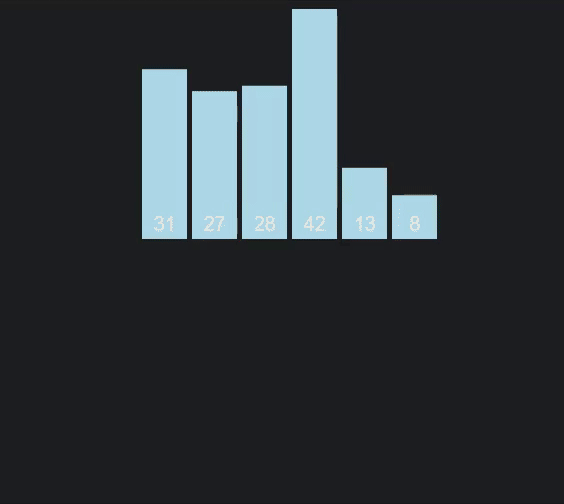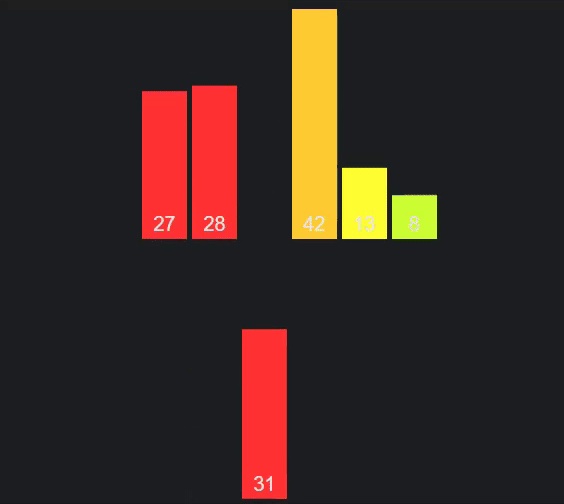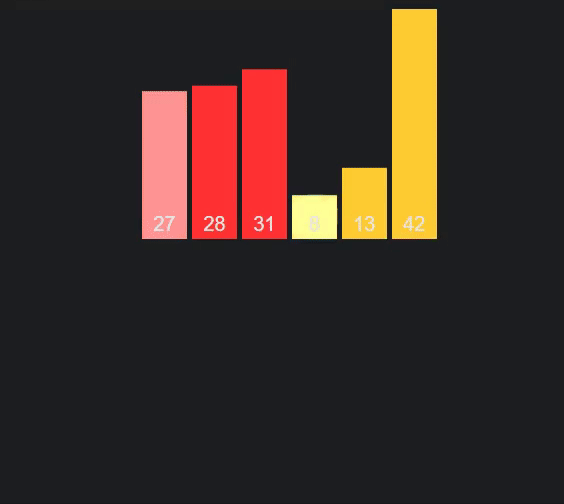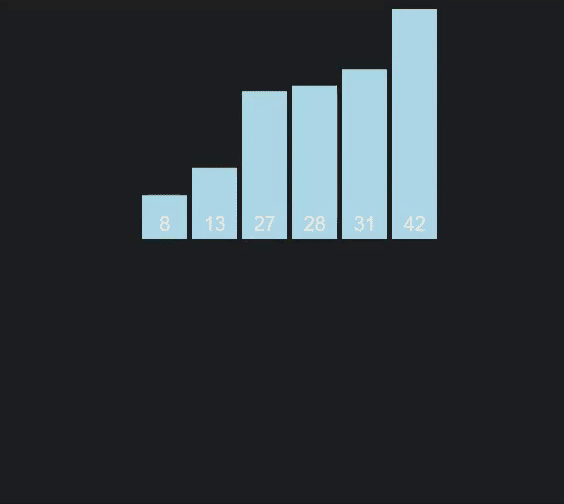
O objetivo aqui passa por partir sucessivamente em metade o vetor de elementos a ordenar, até obtermos vetores com apenas um elemento. Ao chegar a vetores com um só elemento, fazemos merges sucessivos entre dois vetores "vizinhos", de modo a gerar um vetor ordenado a partir de dois outros vetores ordenados - podemos fazê-lo, já que o caso base da recursão, vetores com um só elemento, estão ordenados por natureza. O gif acima pode ser bastante útil a entender o procedimento do algoritmo.

void merge_sort(Item a[], int left, int right) {
    int m = (right + left) / 2;
    if (right <= left) {
        return;
    }
    merge_sort(a, left, m);
    merge_sort(a, m + 1, right);
    merge(a, left, m, right);
}

Item aux[maxN];

void merge(Item a[], int left, int m, int right) {
    int i, j, k;
    for (i = m + 1; i > left; i--) {
        aux[i - 1] = a[i - 1];
    }
    for (j = m; j < right; j++) {
        aux[right + m - j] = a[j + 1];
    }
    for (k = left; k <= right; k++) {
        if (less(aux[j], aux[i]) || i == m + 1) {
            a[k] = aux[j--];
        } else {
            a[k] = aux[i++];
        }
    }
}

Este é o primeiro algoritmo de ordenação de vetores que vimos até agora com pior caso sub-quadrático: a sua complexidade temporal é $O(n\log{n})$ (e também $\Omega(n\log{n})$).

Heap Sort (Enquadramento)

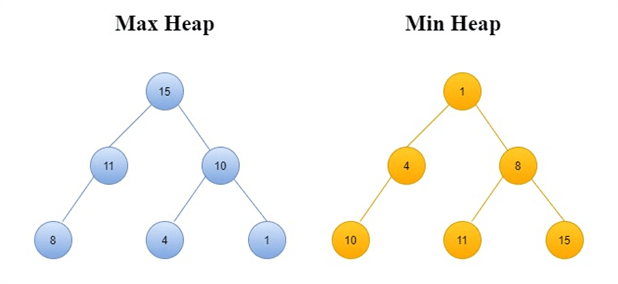
O heap sort utiliza a noção de heap, ou amontoado. A raiz desta estrutura deve conter sempre o menor/maior elemento do vetor (consoante queiramos uma min ou max heap). Considerando o caso em que o maior elemento do vetor é a raiz, podemos definir heap tal que:

Temos, portanto, que neste caso particular nenhum elemento pode ter chave maior que a do seu pai.

A explicação deste algoritmo por palavras não é muito fácil, pelo que preferimos recorrer ao gif abaixo para ajudar à explicação:

Inicialmente, construímos a max heap, que segue o tal princípio de que cada elemento tem chave menor igual à do pai. De seguida, retiramos a raiz do amontoado e colocamo-lo no fim do vetor - esse elemento encontra-se ordenado. Vamos ao último elemento do vetor, dizemos que essa é a nova raiz, e fazemos fix down da heap, de modo a que o maior elemento do amontoado volte a estar presente na raiz. Fazemos este processo sucessivamente até que o amontoado tenha apenas um elemento, estando então ordenado.

void heap_sort(Item a[], int l, int r) {
    build_heap(a, l, r);
    while (r - l > 0) {
        exch(a[l], a[r]);
        fix_down(a, l, --r, l);
    }
}

void build_heap(Item a[], int l, int r) {
    int k, heapsize = r - l + 1;
    for (k = heapsize / 2 - 1; k >= l; k--) {
        fix_down(a, l, r, l + k);
    }
}

void fix_down(Item a[], int l, int r, int k) {
    int ileft, iright, largest = k;
    ileft = l + left(k - l);
    iright = l + right(k - l);
    if (ileft <= r && less(a[largest], a[ileft])) {
        largest = ileft;
    }
    if (iright <= r && less(a[largest], a[iright])) {
        largest = iright;
    }
    if (largest != k) {
        exch(a[k], a[largest]);
        fix_down(a, l, r, largest);
    }
}

int parent(int k) {
    return ((k + 1) / 2) - 1;
}

int left(int k) {
    return 2 * k + 1;
}

int right(int k) {
    return 2 * (k + 1);
}

A construção do amontoado é realizada em tempo sub-quadrático, $O(n \log{n})$ (pode ainda ser provado que é realizada em tempo linear). A colocação das chaves segue a mesma complexidade no pior caso, tal como o próprio algoritmo: o heap sort tem complexidade temporal $O(n\log{n})$. Não é estável.

Mais uma vez, e tal como no final da última página, recomendo consultar a demonstração visual dos algoritmos referidos nesta página.